
In early summer 2008 viewers were reacquainted with sport as drama, beauty and humbling experience in one of the greatest tennis matches played. Rafael Nadal and Roger Federer submitted the exemplar contest from among an embarrassment of options of a modern golden age of tennis. Already trending toward two of the sport’s all-time greats, we witnessed two ruthless and sublime competitors going the distance at the most prestigious tournament, with the added wrinkle of a shake up to add drama to the story.
Viewers were spoiled for close to a decade with matches of similar quality and competitiveness. It is one of many testaments to the Wimbledon 2008 Men’s Final that it continues to stand out. Several factors go into this valuation: the venue, the players, the stakes, the compounding drama of the match itself, the duration, the setting sun adding to the atmosphere, the developing storyline that was incomplete until the final point, all within which both players continued to execute at an elite level.
Five sets in the Wimbledon final with darkness enveloping the action, a shake up, a change of guard type of result. How much closer could it get, what more could we ask for? We were fortunate to watch such performances.
In a tiny, teeny-weeny way we can relive, at least revisit, the match and consider how else it may have played out.
The scoring system is one of many aspects of tennis I find appealing. On first glance it appears a bit quirky but you figure underneath it all it is like other sports, whoever scores the most wins. This is true, to a point. The winner is ultimately the one who wins the two or three sets out of a total of three or five, respectively. The winner of sets has to win games within the set and points within those games.
However, there is no guarantee that the ultimate victor has won the most points out right (nor the most games). If we imagine a close match where the eventual winner has lost all their games at love (meaning without scoring a point) and also been pushed to deuce (tie in points, requiring to win by two) in all the games they have won we can end up with an example of the losing player having accumulated more points despite not carrying the match. Nor do we require such extreme disparities to have this occur.
Further we can end up with an equal number of points for each side though of course we have no draws. It is due to the structure of the scoring that this can occur and while it may seem ridiculous and artificial if you have only now been acquainted with it tennis is hardly the only venue where this occurs. Boxing has this in common with tennis, scoring shots, winning rounds, and taking the fight, with the added option of ending the fight on your own terms if you can pull off the knockout, despite trailing on all cards leading into the final seconds of the final round of the fight (see: Chavez v Taylor I).
This is a cute detail you may think. Just for games, not life. You sure about that? Is not much of our lives a series of contests, competitions between others and within ourselves, structured on social rules and obstacles we have agreed to? E.g., a college degree: lectures, assignments, papers, tests, different courses, a major, and finally a degree. We will win and lose points, games and even sets along the way. In spite of these setbacks we are still able to win the match (that is, get the degree for those keeping score at home) if we spread out the losses and consolidate our wins. In any case, the central point of origin is us as a species (Homo Ludens). That in itself is enough to tie the two together, allowings us to learn from their similarities and differences.
Using crude match-specific stats1 we can re-run the action and see who comes out on top, how often and how close it plays out over the long run. We may view this as an exercise of deterministic beings in a probabilistic world.2 We will take this approach as an implicit “as if” when running these simulated matches of Rafa v Fed.

Above we see a visual representation of 10,000 matches. Fed wins in light color, Rafa in dark. Tough to know what to make of the results based on the vis alone. We see a mixture of both colors, neither appears to dominate, and some clumpiness suggests winning streaks. When looking at actual counts we see that Fed has a 55% win rate. To see if this was robust enough of a finding 10 simulations of 10k matches were run. We see a consistent result:
run 0, Fed win rate: 0.5644
run 1, Fed win rate: 0.5508
run 2, Fed win rate: 0.5663
run 3, Fed win rate: 0.5663
run 4, Fed win rate: 0.5677
run 5, Fed win rate: 0.5582
run 6, Fed win rate: 0.5585
run 7, Fed win rate: 0.5573
run 8, Fed win rate: 0.5533
run 9, Fed win rate: 0.5598
Digging a little deeper to get a profile of the matches we can break out the results by sets needed to win. Here again we see Fed edging out Rafa, across categories:
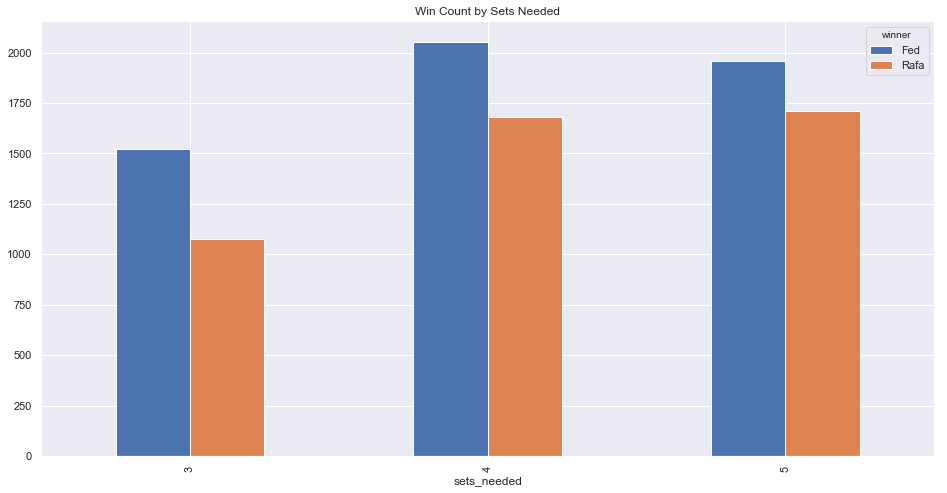
Driving home the point we can also count winnning streaks. We see again an edge for Fed but Rafa’s stats align well and we can see his actual win was no fluke from this perspective. Less so than could be expected from their 2017 Wimbledon final where Fed wins 6966 out of 10k.
winner streak
Fed 1 1138
2 540
3 347
4 193
5 110
6 63
7 30
8 21
9 11
10 6
11 1
13 2
Rafa 1 1348
2 612
3 291
4 113
5 55
6 24
7 9
8 6
9 1
10 2
11 1
The attractiveness of this exercise is in exploring probabilistic outcomes. Given the various percentages and match length involved a straight analytical approach would be insufficient, intractable, or simply not worth the hassle. With these wonderfully useful calculators we may have the heavy lifting done for us, grabbing a glimpse at the possibilities without having to trouble ourselves with carrying all of the ones. More appealing still is the prospect of getting different answers across multiple runs, driving home the point that we are dealing with probabilistic outcomes and hardly with matters of certainty. Once we begin appreciating that various futures are possible there is a certain appeal to the unknown. Not that it rescues our free will necessarily but it certainly piques our attention.
Notes
Opening Photo by Howard Lawrence B on Unsplash
1 The numbers relied on are admittedly a bit blunt. Better would be to have set-specific stats and even deuce/ad side percentages. ↩
2 Michael Lewis and what he learned from writing the undoing project ↩
Code @nbviewer